twierdzenie odwrotne do twierdzenia Pitagorasa

Twierdzenie Pitagorasa opisuje związek między długościami boków trójkąta prostokątnego. Najpierw przyjmujemy, że trójkąt jest prostokątny (musimy mieć pewność, że jest). Potem, przy pomocy dobrze znanego wzoru $a^2+b^2=c^2$, możemy obliczyć długość jednego z boków. Pod warunkiem, że znamy długości dwóch pozostałych.

Twierdzenie odwrotne do twierdzenia Pitagorasa pokazuje, w jaki sposób możemy sprawdzić, czy trójkąt jest prostokątny. W tym celu musimy zmierzyć i porównać długości jego boków. Przepis jest prosty:

1. zmierz długości wszystkich boków trójkąta
2. podnieś je do drugiej potęgi (do kwadratu)
3. dodaj dwie mniejsze liczby do siebie
4. porównaj sumę (wynik dodawania) z trzecią liczbą

Jeśli suma kwadratów długości dwóch krótszych boków jest równa kwadratowi długości najdłuższego boku, to trójkąt jest prostokątny.

przykład

$a^2+b^2=c^2$
$3^2+4^2=5^2$
$9+16=25$
$25=25$
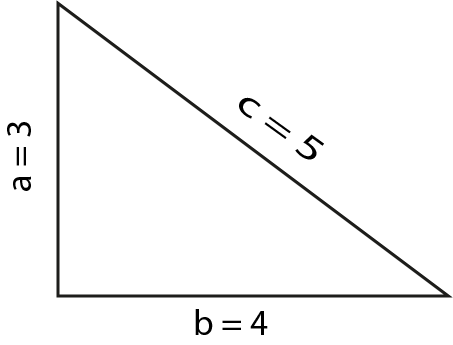
Dlatego mamy pewność, że trójkąt jest prostokątny.

Rozwiązując zadania polegaj na wynikach obliczeń, nie na rysunku. Jeśli trójkąt na ilustracji sprawia wrażenie prostokątnego, ale z obliczeń wynika, że suma kwadratów długości krótszych boków nie jest równa kwadratowi długości najdłuższego boku, to trójkąt nie jest prostokątny. Nawet, jeśli różnica jest minimalna.

Na koniec wyjaśnienie. Używaliśmy określeń "dwa krótsze boki" oraz "najdłuższy bok" zamiast "przyprostokątne" i "przeciwprostokątna" ponieważ początkowo nie wiedzieliśmy, czy trójkąt jest prostokątny. Gdyby okazało się, że nie jest, to używanie słów "przyprostokątne" i "przeciwprostokątna" nie miałoby sensu.