wyprowadzenie wzoru na długość przekątnej kwadratu

Wzór na długość przekątnej kwadratu pojawia się w zadaniach. Można go zapamiętać, ale lepiej zrozumieć skąd się bierze. Dzięki temu łątwiej go zapamiętasz, a jeśli nawet zapomnisz, wyprowadzisz go w minutę lub dwie.

Zacznijmy od kwadratu. To figura geometryczna, która spełnia trzy warunki:

1. jest równoległobokiem
2. wszystkie jej boki mają taką samą długość
3. wszystkie kąty mają miarę 90°, są więc kątami prostymi

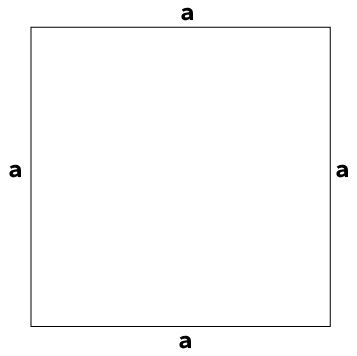
Ponieważ długości boków są jednakowe, możesz uprościć oznaczenia zostawiając tylko jedną literę, np. a

W kwadracie możemy wyznaczyć dwie przekątne. Narysuj jedną z nich i oznacz ją literą, np. d .

Teraz widać, że przekątna podzieliła kwadrat na dwa przystające trójkąty. Przystające, czyli identyczne. Możemy ustawić je w taki sposób, że po nałożeniu jednego na drugi będą idealnie do siebie pasowały. Wybierzmy jeden z nich.

Trójkąt ma następujące właściwości:

1. Jest prostokątny.
2. Jest równoramienny (ponieważ dwa ramiona trójkąta są jednocześnie bokami kwadratu).
3. Boki o jednakowej długości, oznaczone literą a są przyprostokątnymi tego trójkąta.
4. Przekątna kwadratu jest jednocześnie przeciwprostokątną trójkąta.

W trójkącie prostokątnym suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej.

W tym przypadku obie przyprostokątne mają jednakową długość i są oznaczone tą samą literą a. Przeciwprostokątna jest oznaczona literą d.
Możemy zapisać:
$a^2+a^2=d^2$
Dodajemy kwadraty długości przyprostokątnych:
$2a^2=d^2$
Pierwiastkujemy obie strony równania:
$\sqrt{2a^2}=\sqrt{d^2}$
Z prawej strony równania pierwiastek wyciągamy od razu. Z lewej strony korzystamy z tego, że pierwiastek z iloczynu zawsze możemy zapisać jako iloczyn pierwiastków:
$\sqrt{a^2}\sqrt{2}=d$
Ostatecznie dostajemy:
$a\sqrt{2}=d$
Dla porządku zamieniamy równanie stronami:
$d=$ a\sqrt{2}$$
I to jest poszukiwany przez nas wzór na długość przekątnej kwadratu.